|
Outlier identification procedure for reduction of handicaps
D.L. Knuth, F.J. Scheid and F.P. Engel
USGA Handicap Research Team, Far Hills, NJ, USA
Abstract
The USGA Handicap Research Team developed a procedure to identify exceptionally low net tournament scores below a threshold of acceptability. The procedure was implemented in the USGA Handicap System in 1991 to automatically reduce the USGA Handicap Index of any player who has returned two or more exceptional net tournament scores (from special competitions designated by the golf club). This Formula was developed using combinatorial theory, the normal model and sampling theory and tested using empirical data. Tournament scores are tracked for a calendar year and two exceptional tournament scores will be applied to re-compute a lower USGA Handicap Index, overriding the usual USGA Handicap Formula which uses the best 10 of the latest 20 scores.
The process has resulted in lowering the handicaps of one-half of one percent of the 3.4 million American golfers with USGA Handicap Indexes. Reports from golf clubs indicate that those players being reduced are often the same players who previously were dominating handicap composition. The procedure continues to evolve based on research and data analysis.
Key Words. Exceptional Tournament Score, Handicap, Reduction of Handicap, Net Composition.
1. Introduction
The United States Golf Association Handicap Research Team (HRT) has studied the reliability and accuracy of the USGA Handicap System since 1979. Through the introduction of the USGA Course Rating System and the USGA Slope System in 1983, USGA Handicaps have become portable from course-to-course. A remaining problem affecting the reliability of handicaps was that a very small number of golfers would repeatedly score so well in major handicap competitions that it would diminish the enjoyment of the game for the entire field of players. Some of these exceptional performers have been labeled "sandbaggers' or "mug hunters,' but many times honest golfers naturally play better than normal in major competitions.
The HRT undertook a study to determine methods of identifying outlying low scores. These scores were defined by establishing low occurrence rates (1/200) to identify exceptionally low scores and to adjust the handicaps of identified golfers downward to a probably level based on these scores.
The study eventually led to a procedure that was tested widely and then implemented throughout the United States in 1991. This procedure has reduced the handicaps of approximately 16,000 golfers of the 3,400,000 golfers nationwide (0.47%).
2. Defining the Golfer and Equitable Net Competition
USGA research in 1974 by T. Bogevold studied the relationship between handicap level and the odds of scoring low net scores. F.J. Scheid in 1979 conducted research into methods to compare more than 100 handicap systems under various forms of competitions. Research using more than 100,000 scores indicated that golfers' scores could be approximated by the normal model, but that the variability of scores, as measured by the standard deviation, varies widely between golfers and that scores are not symmetrically distributed. Poor scores range farther from the mean than good scores and this is generally more pronounced in less skilled golfers than highly skilled golfers. Partly because of the lack of symmetry, the USGA Handicap System Formula is based on a player's better-half scoring average so that potential ability is the basis of the handicap rather than the player's average performance. Net competitions with many competitors have been termed Large Field Net Events (LFNE) and are dif6cult to handicap equitable even if all player's distributions were identical, which they are not. In a field of 100 players, for example, it can be argued that only one will probably play in the top one hundredth of his score distribution, and in doing so ought to be the winner. This suggests that fair play in LFNE's calls for equalizing the percentile one scores of the competitors, which is not the basis for how players are handicapped. The USGA Handicap Formula came out in Scheid's research as nearly the best formula and was exceeded only slightly by the normal model (The HRT uses mean - 2.326 sigma). In both cases, the median RMS errors were slightly greater than 1.2 stroke. It was concluded that the cause of the error is the fact that the tails of a distribution are hard to define with precision which makes it difficult to arrange fair play in LFNE's. However, the USGA System does better than any other overall when considering that it also does quite well in other forms of play, such as head-to-head match play. Research also indicated that a "Bonus for Excellence" is built into the USGA Handicap System by use of the 96% multiplier and that the multiplier would have to be 113% to make all levels of players equal in individual match play and 101% to equalize net scores in LFNE's to finish in percentile one.
Using a field of 100 golfers playing 36 holes, American players' distribution of handicaps and chances of winning in LFNE's is as follows:
|
Table 1: Probability of Winning LFNE Based on Handicap |
| |
|
% of USA |
Probability |
|
Group |
Handicaps |
Men |
of Winning |
|
A |
10 and under |
23.1 |
.38 |
|
B |
11 to 15 |
26.9 |
.25 |
|
C |
16 to 20 |
22.8 |
.18 |
|
D |
21 and over |
27.1 |
.19 |
Using a new data base from 20,000 golfers from 300 clubs in Massachusetts, in 1980 Scheid found an average RMS error of 1.4 stroke in LFNE's and this result was only one-tenth stroke worse than the normal model, which finished best. The problem of producing equity in LFNE's is further complicated by Scheid's finding that a player's individual scoring variability can make a difference in performance of four strokes. Based on 1985 research, a player with a standard deviation of 5 may be getting two strokes too many, while a steady player with Sigma of two may need two more strokes.
3. Identifying Unusual Sequences of Good Scores
F. P. Engel used Bogsvold's data in 1983 to determine the likelihood of a player's recording a low sum of negative differentials (net score lower than the Course Rating) using combinatorial theory based on number of rounds played. By grouping the scores by sum of the ones that beat the Course Rating, a well defined linear order to the outcomes was used to identify unusually strong performances. The result was a series of tables based on handicap level and number of rounds. For example, players in the handicap range of 14 to 22 in six rounds will have a one in 121 chance that the sum of his negative differentials is equal to or greater than -8. The HRT was concerned with how to relate the seemingly many ways that a player could arrive at a low net sum. For example, one score of -8 would have the same sum as two -4's or four -2's. Since the principle of the USGA Handicap System is and has been to reduce the handicap of a player who consistent scores much better in competitions than in informal games, in 1984 the HRT proposed to consider reducing only golfers with at least two exceptional tournament scores. Engel developed new tables based on the following logic:
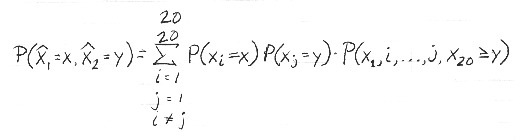
where 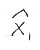 and and 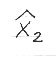 are the lowest two scores for USGA Handicap purpose this simplifies to: are the lowest two scores for USGA Handicap purpose this simplifies to: 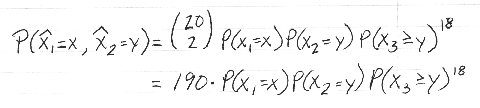
The values in these tables only include pairs of best negative differentials and determines how many strokes a golfer's handicap should be reduced to allow his best two differential likelihood to be an acceptable "rarity." As an example, consider the golfer whose best two differentials of his last 20 scores were -6 and -8 and the player has a handicap of 15. This event would have a 1 in 7,249 chance. If a threshold of 1 in 2S8 was established as the limit of reasonability, this player should have his handicap First reduction procedure introduced to American clubs 231 lowered three strokes (three diagonal steps to the left in Table 2).
Table 2. Probability of Two Best Scores Beating Handicap
| |
0 |
-1 |
-2 |
-3 |
-4 |
-5 |
-6 |
-7 |
-8 |
-9 |
-10 |
|
0 |
27 |
46 |
92 |
199 |
408 |
869 |
1808 |
2480 |
3871 |
9180 |
85779 |
|
-1 |
46 |
13 |
26 |
58 |
118 |
253 |
526 |
722 |
1126 |
2672 |
24967 |
|
-2 |
92 |
26 |
20 |
43 |
89 |
191 |
398 |
546 |
853 |
2023 |
18907 |
|
-3 |
199 |
58 |
43 |
59 |
121 |
258 |
537 |
737 |
1150 |
2728 |
25492 |
|
-4 |
408 |
118 |
89 |
121 |
200 |
427 |
888 |
1219 |
1903 |
4512 |
42163 |
|
-5 |
869 |
253 |
191 |
258 |
427 |
821 |
1708 |
2343 |
3657 |
8672 |
81030 |
|
-6 |
1009 |
526 |
398 |
537 |
888 |
1708 |
3385 |
4644 |
7249 |
17189 |
***** |
|
-7 |
2480 |
722 |
546 |
737 |
1219 |
2343 |
4644 |
6225 |
9716 |
23041 |
***** |
|
-8 |
3871 |
1126 |
853 |
1150 |
1903 |
3657 |
7249 |
9716 |
14912 |
35361 |
***** |
|
-9 |
9180 |
2672 |
2023 |
2728 |
4512 |
8672 |
17189 |
23041 |
35361 |
82951 |
***** |
|
-10 |
85779 |
24967 |
18907 |
25492 |
42163 |
81030 |
***** |
***** |
***** |
***** |
***** |
Tables were produced for five different levels of players. Generally, the odds decrease as handicaps increase because of the increasing variability of scores of higher handicap players.
4. Adopting the Outlier Identification for Tournament Scored
Engel refined his tables in 1985 for use with tournament score identification. Unlike, the CONGU (Council of National Golf Unions) system, the USGA Handicap System uses all scores, whether made in casual rounds or in competitions. "Tournament scores" are special rounds resulting with winners as determined by the Committee and announced in advance. In converting the Outlier identification procedure to one which identifies only tournament scores as the Outliers, the handicap adjustment procedure is complicated by the fact that the adjustment is a function of the actual sequence of tournament score differentials and not just a function of the sum of the negative differentials. Scheid studied net differentials in 1989 by using the normal model and different sets of mean and standard deviation as the basis for scoring performance. His conclusion was that the more reliable mechanism for identification and reduction would be to average a player's two best tournament scores and factoring in the number of tournament scores reported. Having studied combinatorial and the normal model methods of determining Outlier scores, Scheid approached the problem using sampling theory with a sample of 20,000 golfers. His tables agreed closely with Engel's earlier work. He also concluded that to base the acceptance level on a probability of 1/200 makes no sense unless long-term tournament score performance records maintained, because controls are not being enforced well if players are allowed to score "once-in-a-lifetime" tournament scores every twenty rounds. Lowering the acceptance level (error) to say one in 50 instead of one in 200 would penalize many honest players.
5.First Reduction Procedure Introduced to American Clubs
In 1988, the USGA approved including in the Handicap Manual a guideline for golf clubs to mathematically determine handicap reductions. This procedure appeared in the 1989 USGA Handicap System Manual. The first process read as follows:
"Generally, if there are two or more scores among either the player's last 20 scores or any scores made in the current season, and the handicap differentials of the two best tournament scores are at least three strokes better than his USGA Handicap Index, the Committee would be justified in reducing the player's USGA Handicap Index 232 Outlier identification procedure for reduction of handicaps to a value equal to the second-best tournament differential plus three. Example: The USGA Course Rating is 70.6, the Slope Rating is 130 and the player's USGA Handicap Index is 17.6. The player's best two scores in competition are an 82 and 83. The second-best tournament differential is 10.8 (83-70.6 x 113/130 = 10.8). Since this differential is more than three strokes better than 17.6, the Committees would be justified in lowering the player's USGA Handicap Index to 13.8 (10.8+3=13.8)."
This procedure was quickly adopted by major handicap services and was provided as a tournament score tracking service. Golf clubs would identify tournament scores with a "T" next to such scores and the handicap service companies would provide recommended handicap reductions for exceptional players based on the above formula.
Based on Scheid's research, Engel recomputed his probability tables in 1990 to use the average of the best two tournament scores.
6. Automatic Reduction of Handicap Based on T-Scores
By 1990, the number of golfers identified for handicap reduction was in the thousands, but only a small percentage of clubs had taken action to reduce the handicaps of such players. Surveys by state golf associations indicated a desire of the clubs to take action, but a reticence on the club's part to do so. Many clubs asked the USGA to make the reduction procedure automatic and a part of the USGA Handicap Formula.
At a four-day meeting of the HRT in September, 1990, the Committee combined the most recent works of Scheid and Engel to develop a simpli6ed table that would ultimately lead to an automatic procedure that would be included in the 1991 USGA Handicap System Manual for implementation by all golf associations and golf clubs and their computation services by January 1, 1992.
The procedure now in effect can he summarized as follows:
a. Save tournament scores contained within the player's last 20 scores or any made within the current calendar year.
b. If a player has two or more eligible tournament scores (see Section 7a) and at least two tournament score differentials are at least three strokes better than the player's current Handicap Index, proceed to c.
c. Average the two lowest tournament score differentials.
d. Add the result to the following performance limit based on number of T-Scores and round to a tenth:
|
Number of eligible T-Scores |
Performance Limit |
| 2 |
3.0 |
| 3 |
3.5 |
| 4 |
4.0 |
| 5 |
4.3 |
| 6-9* |
4.5 |
| 10-19* |
5.0 |
| 20-29* |
5.5 |
| 30-39* |
6.0 |
| 40 or more* |
6.5 |
*table extension effective January 1, 1995
e. If the resulting value is at least 1.0 less than the original Handicap Index, the result becomes the player's new USGA Handicap Index unless overridden by the club Handicap Committee.
7. Example
A player has a USGA Handicap Index of 17.6, three eligible tournament scores and his lowest two are 82 and 83 scored on a course with a Course Rating of 70.6 and a Slope Rating of 130.
Tournament score differentials are:
(82-70.6) X 113/130 = 9.9
(83-70.6) X 113/130 = 10.8
10.8 is 6.8 less than the 17.6 Index
Average of the best two = 10.35
Performance limit for 3 T-Scores is 3.5, 3.5+10.35 = 13.85, round to 13.9
New USGA Handicap Index is 13.9 instead of 17.6.
8. Concluding Remarks
The support for this procedure has been overwhelming. 92% of 7,200 golf clubs surveyed have responded that the procedure is a good change to the Handicap System and that it identifies the right golfers. The HRT continues to refine the procedure with emphasis on using T-Scores from a moving twelve month window and seeking ways to keep from reducing declining players whose early year tournaments are much better than their current performance. The result of combining the different handicap tables has caused the error to he approximately one in 200 for higher handicap players, one in 300 for average players and one in 400 for low handicap players. Many clubs would like to see the performance limit values reduced so that reductions are greater with an error level of approximately one in 100.
9. References
Bogevold, T. (1974) Computer Assisted Handicap Survey, USGA
Engel, F.P. (1983) Identifying Unusual Sequences of Good Scores, USGA
Engel, F.P. (1984) Handicap Adjustments Under Section 8-3, USGA
Engel, F.P. (1985) Arresting the Sandbagger via T-Scores, USGA
Engel, F.P. (199O) Best Two T-Scores Analysis, USGA
Scheid, F.J. (1979) The Search For the Perfect Handicap, USGA
Scheid, F.J. (1979) Golf Competitions Between Individuals, USGA
Scheid, F.J. (1980) The Search For the Perfect Handicap, Part II, USGA
Scheid, F.J. (1985) A Note on Handicapping Error and Sigma, USGA
Scheid, F.J. (1989) Average of Two Best T-Scores, USGA
Scheid, F.J. (1989) T-Scores Follow-Up, USGA
Science and Golf II: Proceedings of the World Scientific Congress of Golf. Edited by A.J. Cochran and M.R. Farrally, Published in 1994 by E & FN Spon, London, ISBN 0 419 18790 1
|




